15.2: Reference Frames and Relative Velocities

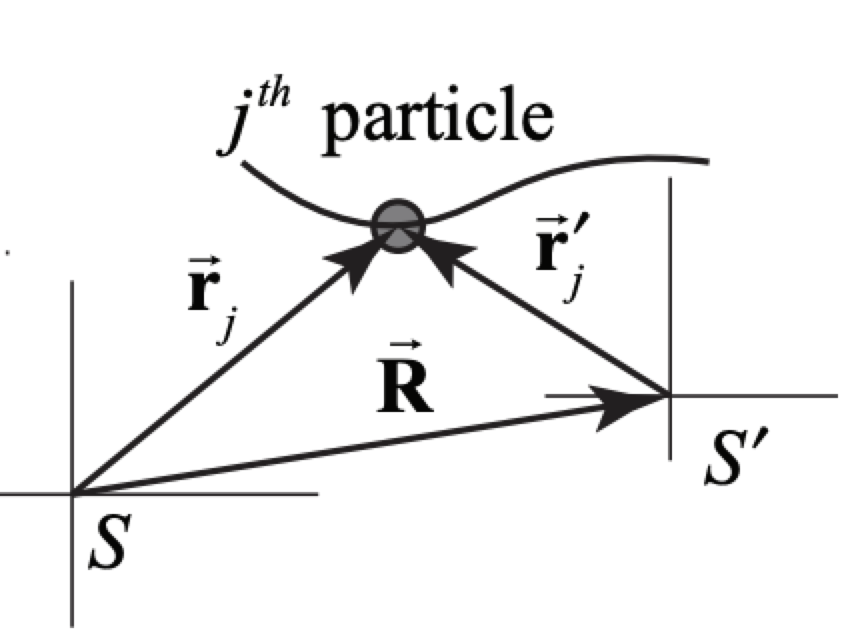
clipboard_e329f14fa0fac24961e40362a090f359d.png

We shall recall our definition of relative inertial reference frames. Let \(\overrightarrow<\mathbf>\) be the vector from the origin of frame \(S\) to the origin of reference frame S′. Denote the position vector of the \(j^>\) particle with respect to the origin of reference frame \(S\) by \(\overrightarrow<\mathbf>_\) and similarly, denote the position vector of the particle with respect to the origin of reference frame \(S^<\prime>\) by \(\overrightarrow<\mathbf>_^<\prime>\)(Figure 15.1). The position vectors are related by \[\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf> \nonumber \] The relative velocity (call this the boost velocity) between the two reference frames is given by \[\overrightarrow<\mathbf>=\frac>> \nonumber \] Assume the boost velocity between the two reference frames is constant. Then, the relative acceleration between the two reference frames is zero, \[\overrightarrow<\mathbf>=\frac>>=\overrightarrow<\mathbf<0>> \nonumber \] When Equation (15.2.3) is satisfied, the reference frames \(S\) and S′ are called relatively inertial reference frames. Suppose the \(j^>\) particle in Figure 15.1 is moving; then observers in different reference frames will measure different velocities. Denote the velocity of \(j^>\) particle in frame \(S\) by \(\overrightarrow<\mathbf>_=d \overrightarrow<\mathbf>_ / d t\), and the velocity of the same particle in frame S′ by \(\overrightarrow<\mathbf>_^<\prime>=d \overrightarrow<\mathbf>_^ <\prime>/ d t\). Taking derivative, the velocities of the particles in two different reference frames are related according to \[\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf> \nonumber \]

Relative Velocities

Consider two particles of masses \(m_<1>\) and \(m_\) interacting via some force (Figure 15.2). 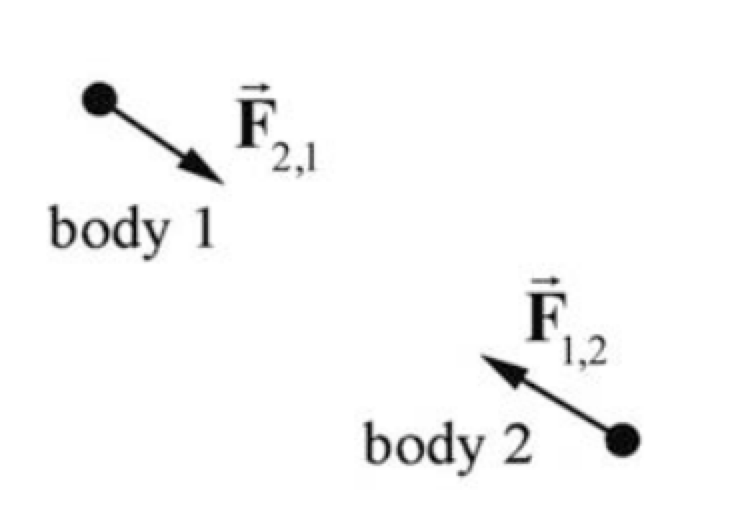clipboard_e36b8ac4800c75e489ee7e459e8c91c1c.pngChoose a coordinate system (Figure 15.3) in which the position vector of body 1 is given by \(\overrightarrow<\mathbf>_<1>\) and the position vector of body 2 is given by \(\overrightarrow<\mathbf>_\) The relative position of body 1 with respect to body 2 is given by \(\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_<1>-\overrightarrow<\mathbf>_\) 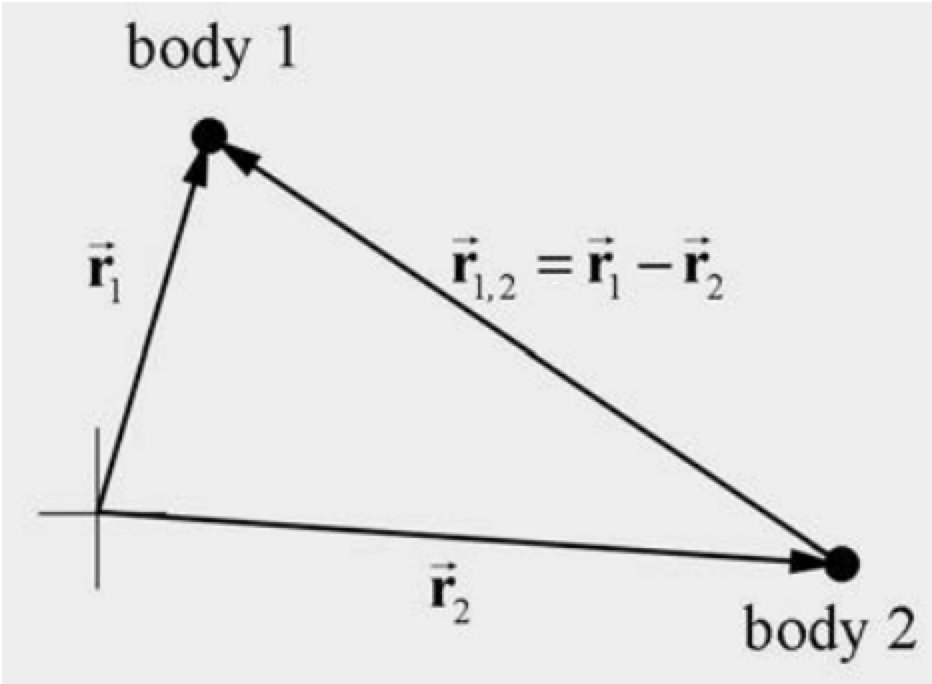clipboard_e4e3c1e7613fff971ef1d35af7866c4d3.pngDuring the course of the interaction, body 1 is displaced by \(d \overrightarrow<\mathbf>_<1>\) and body 2 is displaced by \(d \overrightarrow<\mathbf>_\) so the relative displacement of the two bodies during the interaction is given by \(d \overrightarrow<\mathbf>_=d \overrightarrow<\mathbf>_<1>-d \overrightarrow<\mathbf>_\). The relative velocity between the particles is \[ \overrightarrow<\mathbf>_=\frac>_>=\frac>_<1>>-\frac>_>=\overrightarrow<\mathbf>_<1>-\overrightarrow<\mathbf>_ \nonumber \] We shall now show that the relative velocity between the two particles is independent of the choice of reference frame providing that the reference frames are relatively inertial. The relative velocity \(\overrightarrow<\mathbf>_^<\prime>\) in reference frame S′ can be determined from using Equation 12 (15.2.4) to express Equation (15.2.5) in terms of the velocities in the reference frame S′, \[\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_<1>-\overrightarrow<\mathbf>_=\left(\overrightarrow<\mathbf>_<1>^<\prime>+\overrightarrow<\mathbf>\right)-\left(\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf>\right)=\overrightarrow<\mathbf>_<1>^<\prime>-\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_^ <\prime>\nonumber \] and is equal to the relative velocity in frame S. For a two-particle interaction, the relative velocity between the two vectors is independent of the choice of relatively inertial reference frames

Center-of-mass Reference Frame

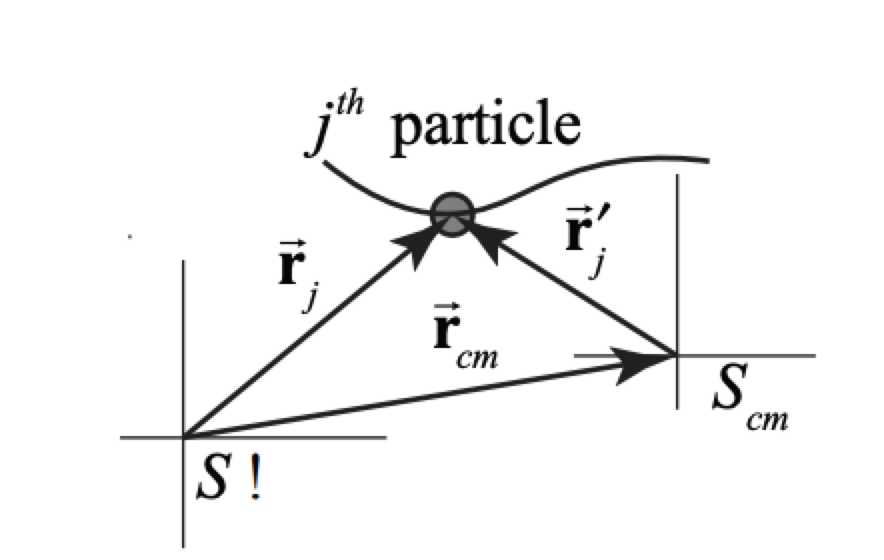
clipboard_ecdc7432af27ee4a49639df4834a675e2.png

Let \(\overrightarrow<\mathbf>_\) be the vector from the origin of frame \(S\) to the center-of-mass of the system of particles, a point that we will choose as the origin of reference frame \(S_\), called the center-of-mass reference frame. Denote the position vector of the \(j^>\)particle with respect to origin of reference frame \(S\) by \(\overrightarrow<\mathbf>_\) and similarly, denote the position of the \(j^>\) vector of the particle with respect to origin of reference frame \(S_\) by \(\overrightarrow<\mathbf>_^<\prime>\). (Figure 15.4) The position vector of the \(j^>\) particle in the center-of-mass frame is then given by \[\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_ \nonumber \] The velocity of the \(j^>\) particle in the center-of-mass reference frame is then given by \[\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_ \nonumber \] There are many collision problems in which the center-of-mass reference frame is the most convenient reference frame to analyze the collision. Consider a system consisting of two particles, which we shall refer to as particle 1 and particle 2. We can use Equation (15.2.8) to determine the velocities of particles 1 and 2 in the center-of-mass, \[\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_-\frac >_+m_ \overrightarrow<\mathbf>_>=\frac\left(\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_\right)=\frac<\mu> \overrightarrow<\mathbf>_ \nonumber \] where \(\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_\) is the relative velocity of particle 1 with respect to particle 2 . A similar result holds for particle 2: \[\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_=\overrightarrow<\mathbf>_-\frac >_+m_ \overrightarrow<\mathbf>_>=-\frac\left(\overrightarrow<\mathbf>_-\overrightarrow<\mathbf>_\right)=-\frac<\mu> \overrightarrow<\mathbf>_ \nonumber \] The momentum of the system the center-of-mass reference frame is zero as we expect, \[m_ \overrightarrow<\mathbf>_^<\prime>+m_ \overrightarrow<\mathbf>_^<\prime>=\mu \overrightarrow<\mathbf>_-\mu \overrightarrow<\mathbf>_=\overrightarrow<\mathbf<0>> \nonumber \]

Kinetic Energy in the Center-of-Mass Reference Frame

The kinetic energy in the center of mass reference frame is given by \[K_=\frac m_ \overrightarrow<\mathbf>_^ <\prime>\cdot \overrightarrow<\mathbf>_^<\prime>+\frac m_ \overrightarrow<\mathbf>_^ <\prime>\cdot \overrightarrow<\mathbf>_^ <\prime>\nonumber \] We now use Equations (15.2.9) and (15.2.10) to rewrite the kinetic energy in terms of the relative velocity \(\overrightarrow<\mathbf>_^<\prime>=\overrightarrow<\mathbf>_^<\prime>-\overrightarrow<\mathbf>_^<\prime>\), \[K_=\frac m_\left(\frac<\mu> \overrightarrow<\mathbf>_\right) \cdot\left(\frac<\mu> \overrightarrow<\mathbf>_\right)+\frac m_\left(-\frac<\mu> \overrightarrow<\mathbf>_\right) \cdot\left(-\frac<\mu> \overrightarrow<\mathbf>_\right) =\frac \mu^ \overrightarrow<\mathbf>_ \cdot \overrightarrow<\mathbf>_\left(\frac+\frac\right)=\frac \mu v_^
\nonumber \] where we used the fact that we defined the reduced mass by \[\frac <\mu>\equiv \frac+\frac \nonumber \]

Change of Kinetic Energy and Relatively Inertial Reference Frames

The kinetic energy of the two particles in reference frame \(S\) is given by \[K_=\frac m_ v_^+\frac m_ v_^ \nonumber \] We can take the scalar product of Equation (15.2.8) to rewrite Equation (15.2.15) as \[\begin
K_=\frac m_\left(\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf>_\right) \cdot\left(\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf>_\right)+\frac m_\left(\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf>_\right) \cdot\left(\overrightarrow<\mathbf>_^<\prime>+\overrightarrow<\mathbf>_\right) \\
=\frac m_ v_^<\prime 2>+\frac m_ v_^<\prime 2>+\frac\left(m_+m_\right) v_^+\left(m_ \overrightarrow<\mathbf>_^<\prime>+m_ \overrightarrow<\mathbf>_^<\prime>\right) \cdot \overrightarrow<\mathbf>_
\end \nonumber \] The last term is zero due to the fact that the momentum of the system in the center of mass reference frame is zero (Equation (15.2.11)). Therefore Equation (15.2.16) becomes \[ K_=\frac m_ v_^<\prime 2>+\frac m_ v_^<\prime 2>+\frac\left(m_+m_\right) v_^ \nonumber \] The first two terms correspond to the kinetic energy in the center of mass frame, thus the kinetic energies in the two reference frames are related by \[K_=K_+\frac\left(m_+m_\right) v_^ \nonumber \] We now use Equation (15.2.13) to rewrite Equation (15.2.18) as \[K_=\frac \mu \nu_^+\frac\left(m_+m_\right) v_^ \nonumber \] Even though kinetic energy is a reference frame dependent quantity, because the second term in Equation (15.2.19) is a constant, the change in kinetic energy in either reference frame is equal to \[\Delta K=\frac \mu\left(\left(v_^\right)_-\left(v_^\right)_\right) \nonumber \] This generalizes to any two relatively inertial reference frames because the relative velocity is a reference frame independent quantity, the change in kinetic energy is independent of the choice of relatively inertial reference frames. We showed in Appendix 13A that when two particles of masses \(m_\) and \(m_\) interact, the work done by the interaction force is equal to \[W=\frac \mu\left(\left(v_^\right)_-\left(v_^\right)_\right) \nonumber \] Hence we explicitly verified that for our two-particle system \[W=\Delta K_ \nonumber \]

This page titled 15.2: Reference Frames and Relative Velocities is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Peter Dourmashkin (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform.

  1. Back to top
    • 15.1: Introduction to Collision Theory
    • 15.3: Characterizing Collisions